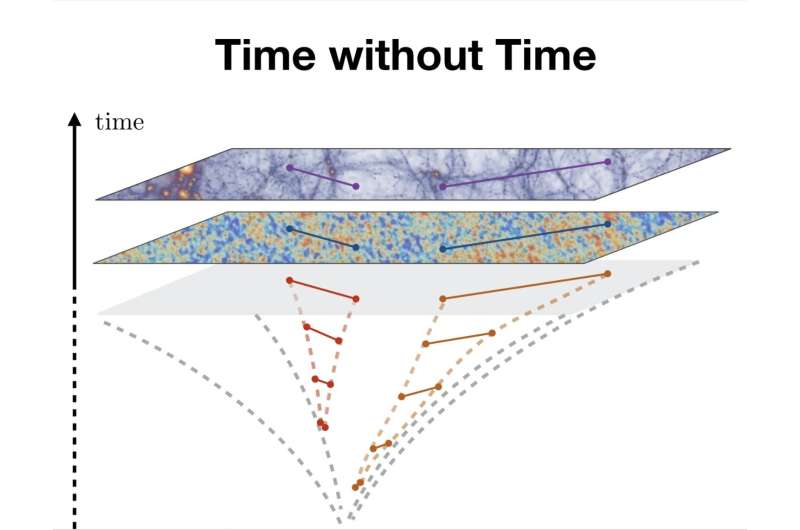
Figura ilustron idenë kryesore pas studimit. Konkretisht, ajo paraqet një pamje “pa kohë” të kozmologjisë së universit të hershëm. Ekipi plotësoi kronologjinë e universit para sipërfaqes gri me këtë ide të korrelacioneve që zgjaten më shumë ose më pak gjatë një faze të hershme të universit.
Kredi: Krijuar nga Guilherme Leite Pimentel, duke përdorur pamje të CMB të marra nga sateliti Planck (ESA). Pjesa e sipërme është nga simulimi Millennium (i mbajtur në Institutin Max Planck për Astrofizikë).
Për të studiuar origjinën dhe evolucionin e universit, fizikantët mbështeten në teori që përshkruajnë marrëdhëniet statistikore midis ngjarjeve ose fushave të ndryshme në hapësirë-kohë, të njohura në mënyrë të përgjithshme si korrelacione kozmologjike. Parametrat kinematikë janë në thelb të dhëna që specifikojnë një korrelacion kozmologjik—pozicionet e grimcave ose numrat e valëve të fluktuacioneve kozmologjike.
Ndryshimet në korrelacionet kozmologjike të ndikuara nga variacionet në parametrat kinematikë mund të përshkruhen duke përdorur të ashtuquajturat ekuacione diferenciale. Këto janë një lloj ekuacionesh matematikore që lidhin një funksion (dmth., një marrëdhënie midis një hyrje dhe një dalje) me normën e tij të ndryshimit. Në fizikë, këto ekuacione përdoren gjerësisht pasi ato janë të përshtatshme për të kapur natyrën shumë dinamike të universit.
Studiues në Institutin për Studime të Avancuara në Princeton, Qendrën Leung për Kozmologji dhe Astrofizikë të Grimcave në Taipei, Institutin Walter Burke për Fizikë Teorike në Caltech, Universitetin e Çikagos dhe Scuola Normale Superiore në Pisa prezantuan kohët e fundit një perspektivë të re për t’iu qasur ekuacioneve që përshkruajnë se si korrelacionet kozmologjike ndikohen nga ndryshime të buta në parametrat kinematikë.
Artikulli i tyre, i botuar në Physical Review Letters, prezanton një kornizë të quajtur “rrjedha kinematike” (kinematic flow), e cila mund të ndihmojë në nxjerrjen e këtyre ekuacioneve diferenciale nga rregulla të thjeshta kombinatorike (dmth., parime për të përcaktuar numrin e mënyrave në të cilat objektet në një grup mund të renditen ose të zgjidhen).
“Filluam të punojmë për këtë artikull rreth shtatorit 2020,” tha Guilherme Leite Pimentel, një nga autorët e artikullit për Phys.org. “Motivimi ynë ishte të kuptonim pse kjo strukturë matematikore—ekuacione diferenciale në hapësirën kinematike—shfaqej vazhdimisht në kozmologji.
“A ishte për shkak të simetrisë? Apo për një arsye më të thjeshtë? Kishim dyshimin se po zëvendësonim evolucionin kohor me ndarjen hapësinore—ideja ishte që një vështrim në një ‘moment’ të universit të hershëm në distanca të mëdha mund të na tregonte për fazat më të hershme të tij—dhe donim ta bënim këtë të saktë.”
Gjatë dekadave të fundit, ekuacionet në hapësirën kinematike janë treguar të dobishme për të parashikuar atë që mund të ketë ndodhur në ditët e para të universit, më shumë sesa qasjet që përfshijnë ndërtimin e një kronologjie të mundshme dhe zhvillimin e saj. Meqenëse qasje të ngjashme janë përdorur edhe nga fizikantët e grimcave, Pimentel dhe kolegët e tij u përpoqën të aplikonin disa nga konstruktet e përdorura në atë fushë për problemin kozmologjik që ishte në qendër të studimit të tyre.
“Historia që tregohet në artikull lindi kur numri i ekuacioneve filloi të bëhej shumë i madh,” tha Pimentel. “Për të ndjekur se çfarë po ndodhte, vendosëm të vizatonim figura të termave në ekuacione, në vend që të shkruanim formula. Duke i parë këto figura, u bë e qartë se kishte një model. Figurave ‘u jepje jetë’ dhe mund të parashikoje ekuacionet përmes një grupi të thjeshtë rregullash që përfshinin prerje dhe ngjyrosje.”
Në analizat e tyre teorike, studiuesit së pari konsideruan hapësirën kinematike të një korrelatori të caktuar (dmth., një mjet për të matur forcën e një marrëdhënieje midis dy madhësive). Më pas, ata zbatuan një grup rregullash ndaj këtij korrelatori.
“Ideja ka disa pjesë: së pari, ne konsiderojmë hapësirën kinematike të një korrelatori të caktuar. Pastaj, zbatuam një grup rregullash ndaj tij: ‘E preme, vizatuam tuba (ose, në mënyrë alternative, e trianguluam) dhe pastaj zbatuam një recetë në dukje ezoterike të rritjes së këtyre tubave, bashkimit të tyre, përthithjes, etj.’,” shpjegoi Pimentel.
“Nëse pranon këto rregulla, atëherë mund të parashikosh të gjitha termat që shfaqen në një familje ekuacionesh matematikisht të qëndrueshme. Zgjidhjet e këtyre ekuacioneve—të cilat varen vetëm nga ndarjet hapësinore, ose kinematika e korrelatorëve—janë integrale në kohë. Në këtë kuptim, koha del në pah. Shfaqja e kësaj strukture tregon se ka mënyra të tjera për të organizuar këto llogaritje, pa përfshirë evolucionin kohor eksplicit.”
Ky punim i fundit nga Pimentel dhe kolegët e tij prezanton një qasje më të thjeshtë për të kuptuar dhe përshkruar korrelacionet kozmologjike komplekse. Korniza e propozuar përputhet me tema të tjera të rrënjosura në gravitetin kuantik, si përdorimi i vëzhgimeve në kufi dhe dalja e hapësirë-kohës, dhe mund të kontribuojë potencialisht në një përshkrim të “pa kohë” të kozmologjisë.
“Prezantuam një grup të ri teknikash për të llogaritur korrelatorët kozmologjikë të universit të hershëm, duke huazuar nga fusha të tjera të fizikës teorike,” tha Pimentel.
“Presim që shumë nga këto teknika të jenë gjerësisht të aplikueshme, përtej modeleve të thjeshta që përshkruam në letrën tonë. Përdorimi i teknikave nga fusha të tjera ngjalli interesin e matematikanëve dhe fizikantëve të grimcave, të cilët po kërkojnë mënyra për të kontribuar me përvojën e tyre. Këto lidhje tregojnë se ka gjasa që të ekzistojë më shumë dije që mund të shfrytëzohet midis këtyre fushave.”
Ky punim i fundit i ekipit mund të frymëzojë së shpejti studime të tjera teorike që ndërtojnë mbi kornizën që ata prezantuan. Ndërkohë, Pimentel dhe kolegët e tij po kërkojnë shembuj të tjerë ku koncepti i tyre i “rrjedhës kinematike” mund të shfaqet dhe po mendojnë për modele më të sofistikuara për kërkime të mëtejshme.
“Në studimet tona të ardhshme, mund të aplikojmë këto teknika edhe në modele që i afrohen më shumë asaj që presim të ketë qenë universi i hershëm,” tha Pimentel.
“Një tjetër kufi për kërkime të ardhshme do të jetë të shtyjmë përtej termit dominues—duke kaluar nga pemët te lakoret—ku shfaqen shumë sfida të reja teorike dhe matematikore. Jam gjithashtu thellësisht i angazhuar në gjetjen e një përshkrimi të ri të grimcave me rrotullim në kozmologji, ku po shohim shenja të strukturave të reja matematikore që janë paraqitur më parë edhe në fizikën e grimcave.”
Përmbledhje
Çfarë janë “korrelacionet kozmologjike”?
Këto janë lidhje midis ngjarjeve ose gjërave që ndodhën në pjesë të ndryshme të universit, si për shembull si u shpërndanë grimcat në Big Bang ose si drita nga ato kohë arriti deri tek ne. Këto lidhje na ndihmojnë të kuptojmë si u krijua dhe si është zhvilluar universi.
Çfarë janë “parametrat kinematikë”?
Janë të dhëna që përshkruajnë lëvizjen ose pozicionin e gjërave, si vendndodhja e grimcave ose sa valë ka një fushë energjie në univers. Kur këto ndryshojnë, ndryshojnë edhe lidhjet midis gjërave në univers.
Çfarë kanë bërë shkencëtarët?
Ata kanë zbuluar një mënyrë të re për të përshkruar këto ndryshime, të quajtur “rrjedha kinematike” (kinematic flow).
Kjo metodë ndihmon që ekuacionet (dmth. llogaritjet matematikore) që përshkruajnë lidhjet në univers të nxirren më lehtë, jo duke ndjekur kohën, por duke parë distancat në hapësirë.
Pse është kjo e rëndësishme?
Normalisht, për të kuptuar universin e hershëm, ne mendojmë se gjithçka ndodhi në një rend kohor: fillimi, pastaj një fazë tjetër, dhe kështu me radhë. Por kjo mënyrë e re tregon se ndoshta mund të kuptojmë gjithçka pa pasur nevojë për një kohë të rrjedhshme—thjesht duke parë si janë të lidhura pjesët e ndryshme të universit në një moment të vetëm.
Si e zbuluan këtë?
Kur po punonin me shumë ekuacione të vështira, shkencëtarët filluan të vizatonin figura për të kuptuar më mirë se çfarë po ndodhte. Duke parë këto figura, ata vunë re se kishte një model të përsëritur.
Ata krijuan rregulla të thjeshta vizuale për të parashikuar se çfarë do të ndodhte me ekuacionet. Me pak fjalë: nëse ndjek këto rregulla për vizatimet, mund të marrësh ekuacionet pa bërë llogaritje të vështira.
Çfarë përfitojmë nga kjo?
Kjo qasje e re:
-
E bën më të lehtë të kuptojmë si u formua universi.
-
Nuk ka nevojë për një kohë që rrjedh—koha “shfaqet” vetë në fund të llogaritjeve.
-
Mund të ndihmojë në bashkimin e ideve nga fusha të ndryshme si matematika, fizika e grimcave dhe kozmologjia.
Çfarë do të bëjnë më tej?
Studiuesit duan të:
-
Përdorin këtë metodë në modele më afër realitetit të universit të hershëm.
-
Kalojnë nga llogaritjet më të thjeshta (“pemë”) në ato më të ndërlikuara (“lakore”), ku hasen më shumë sfida.
-
Studiojnë grimca që rrotullohen (spinning particles) në universin e hershëm dhe shpresojnë të zbulojnë struktura të reja matematikore.